Area Of Square Prism Formula

SURFACE Expanse OF PRISM AND PYRAMID

Both prism and pyramid are basically 3D shapes. Even though we take different formulas to notice surface expanse of prism and pyramid, the basic thought of finding surface area is to add the areas of all the faces.

First, permit the states wait at, how to find surface area of a prism.

Surface area of Prism

Let usa consider the rectangle prism given beneath.

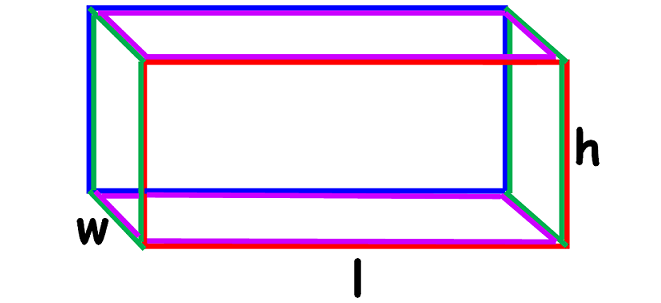
Here is the bones idea to observe area of the above rectangular prism.

Surface Area = Sum of areas of all six faces

Let united states of america discover the area of each confront separately.

Area of the front face (red colored) = l x h

Surface area of the dorsum face (blueish colored) = l x h

Area of the left side face (light-green colored) = w x h

Area of the right side face (greenish colored) = w 10 h

Area of the top portion (purple colored) = l x w

Area of the base (purple colored) = l x w

At present,

Surface area = lh + lh + wh + wh + lw + lw

Expanse = 2lh + 2wh + 2lw

Surface expanse = 2(lh + wh + lw)

This is the formula to find surface surface area of a rectangular prism.

Annotation :

Rectangular prism is also known as cuboid.

We can apply the to a higher place explained basic idea to find area of whatsoever prism without remembering the formulas.

Let u.s.a. find surface area of the cube given below.

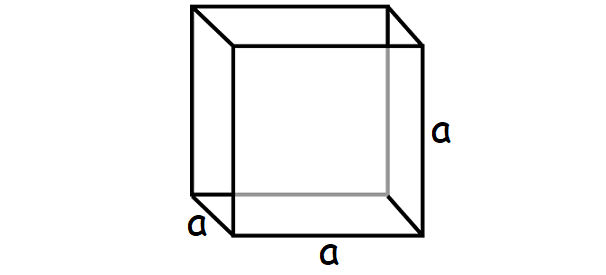
We know that the shape of each face of a cube is a square.

In the above cube, the side length of each face is 'a'.

Then, surface area of each face (square) = a ten a = a².

Therefore,

Surface surface area of cube = 6 x area of each face

Surface expanse of cube = 6a²

Now, let us find surface area of the triangular prism given below.

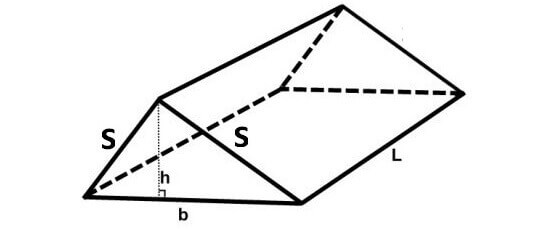
In the above triangular prism, at that place are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side is triangle.

For the given triangular prism,

Area of the base = Lb

Area of the commencement slanting face = Ls

Area of the other slanting face = Ls

Surface area of the front end confront = (1/two)bh

Area of the back confront = (1/2)bh

So,

surface expanse = sum of the area of 5 faces

surface area = Lb + 2Ls + ii ten (1/2)bh

Surface surface area of triangular prism = Lb+2Ls+bh

At present permit the states expect at, how to find surface surface area of a prism.

Surface Area of Pyramid

Let united states consider the pyramid with square base of operations given below.

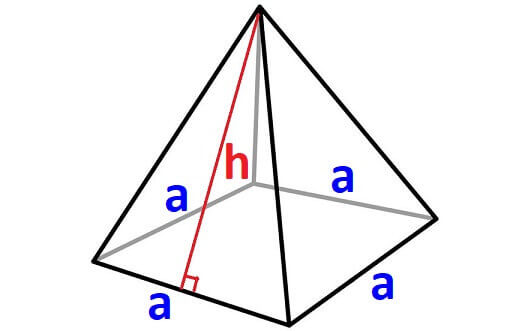
Hither is the basic idea to find surface expanse of the above pyramid.

Area = Sum of areas of all v faces (Including the base)

For any pyramid, if the shape of the base of operations is square, then we will have iv side walls. The shape of each side wall will be a triangle with equal area.

In the above pyramid, the base is a square with side length 'a' a nd each wall is a triangle with base 'a' and height 'h'.

Allow the states find the expanse of each face up separately.

Expanse of the base = a x a = a^two

Surface area of each side wall = (i/2)ah

Expanse of all iv side walls = four x (1/ii)ah = 2ah

Surface area of the above pyramid is

= a^two + 2ah

This is the formula to observe area of a pyramid with square base.

We tin can apply the above explained basic idea to observe area of a pyramid with triangular base.

Let us find surface area of a pyramid with triangular base.

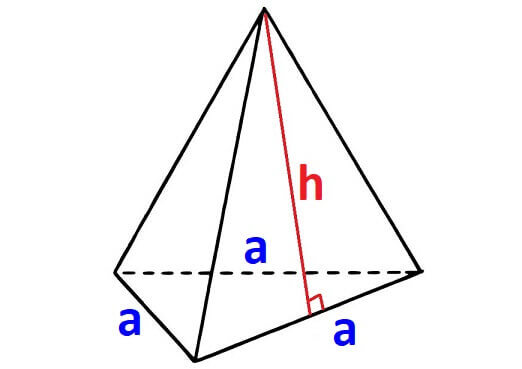
For any pyramid, if the shape of the base is equilateral triangle, then nosotros will accept three side walls. The shape of each side wall will be a triangle with equal surface area.

In the above pyramid, the base is an equilateral triangle with side length 'a'.

And each wall is a triangle with base 'a' and height 'h'.

Let us find the area of each face separately.

Area of the base of operations = ( √iii/4) aⁱⁱ

Surface area of each side wall = (1/2)ah

Area of all three side walls = 3 x (one/2)ah = (iii/ii)ah

Surface area of the above pyramid is

= ( √3/4) a² + (3/ii)ah

This is the formula to detect surface expanse of a pyramid with equilateral triangle base.

Annotation :

If the base of operations is not equilateral triangle and it is either scalene triangle or isosceles triangle, then the area of side walls will not be equal. We accept to notice area of each side wall separately.

Solved Problems

Problem ane :

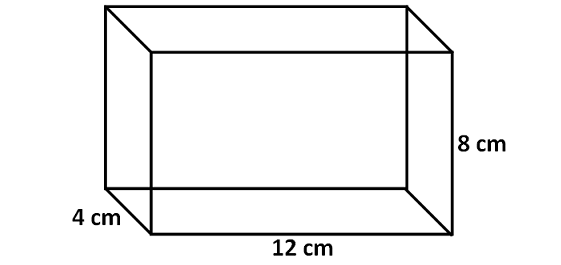
Notice the surface area of the cuboid shown below.

Solution :

Surface area of cuboid is

= Sum of areas of all vi faces

In cuboid, each confront is a rectangle. So we tin can utilise area of rectangle formula to become area of each face.

Area of the forepart face up = 8 x 12 = 96 cm ^two

Area of the back face = 8 x 12 = 96 cm ²

Surface area of the left side face = four x 8 = 32 cm ²

Area of the right side face = 4 10 viii = 32 cm ²

Area of the height portion = 4 x 12 = 48 cm ²

Expanse of the base = 4 x 12 = 48 cm ²

Surface area of the above cuboid is

= Sum of areas of all six faces

= 96 + 96 + 32 + 32 + 48 + 48

= 352 cm²

Alternative Method :

We can use the formula given beneath to detect expanse of cuboid.

Formula for surface area of cuboid is

= two(lh + wh + lw)

Substitute fifty = 12, w = 4 and h = 8.

= ii(12x8 + 4x8 + 12x4)

= ii(96 + 32 + 48)

= 2(176)

= 352 cm²

Trouble ii :

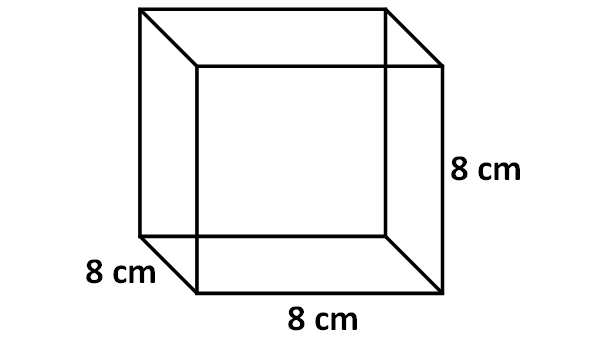
Find the surface area of the cube shown below.

Solution :

We know that the shape of each face up of a cube is a square.

In the above cube, the side length of each confront is "viii".

So, expanse of each face (foursquare) is

= 8 x viii

= 64 cm²

Therefore, surface area of the cube is

= 6 ten area of each face

= 6 x 64

= 384 sq.cm

Problem 3 :

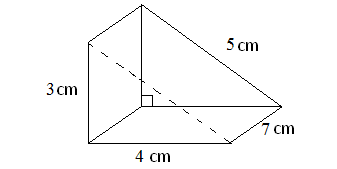
Detect the surface area of the triangular prism shown below.

Solution :

In the above triangular prism, at that place are 5 faces. The shape of the base of operations, vertical confront and slanting face is rectangle. The shape of two faces on the left side and right side is triangle.

For the given triangular prism,

Area of the base = 7 x 4 = 28 cm ²

Expanse of the vertical face up = 3 x 7 = 21 cm ²

Area of the slanting face = five x seven = 35 cm ²

Area of the forepart face = (one/ii) x four x 3 = 6 cm ²

Surface area of the back face = (1/2) x 4 x 3 = 6 cm ^two

So, expanse of the in a higher place triangular prism is

= sum of the expanse of 5 faces

= 28 + 21 + 35 + 6 + 6

= 96 cmⁱⁱ

Problem 4 :

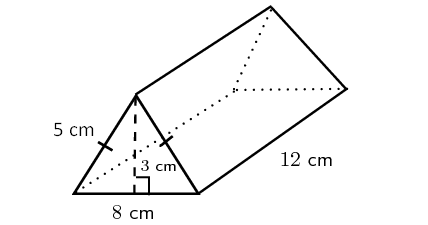
Find the surface surface area of the triangular prism shown below.

Solution :

In the above triangular prism, there are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side is triangle.

For the given triangular prism,

Area of the base = 8 x 12 = 96 cm ²

Area of the first slanting face = 12 x five = lx cm ²

Surface area of the other slanting face = 12 ten 5 = 60 cm ^two

Area of the front end face up = (ane/2) x 8 x 3 = 12 cm ⁱⁱ

Surface area of the dorsum face = (1/two) x 8 x 3 = 12 cm ²

So, surface area of the to a higher place the triangular prism is

= sum of the area of 5 faces

= 96 + 60 + 60 + 12 + 12

= 240 cm²

Problem 5 :

Find the surface expanse of the pyramid shown below.

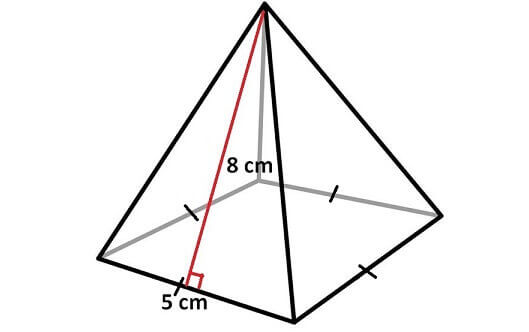
Solution :

Surface area of the pyramid is

= Sum of areas of all 5 faces

In the above pyramid, the base is a square with side length five cm and each wall is a triangle with base 5 cm and height 8 cm.

Let us find the area of each confront separately.

Area of the base of operations = 5 x 5 = 25 sq.cm

Surface area of each side wall = (1/2) x 5 x 8 = 20 sq.cm

Area of all iv side walls = 4 10 20 = 80 sq.cm

Surface area of the above pyramid is

= 25 + 80

= 105 sq.cm

Kindly post your feedback tov4formath@gmail.com

We always capeesh your feedback.